Llamamos ceros o raíces de una función f a los valores de x para los cuales se cumple que f(x)=0. Los ceros de una función son las abscisas de los puntos en los cuales su gráfica tiene contacto con el eje de las x.
En matemática, se conoce como raíz (o cero) de una función (definida sobre un cierto cuerpo algebraico) f(x) a todo elemento xperteneciente al dominio de dicha función tal que se cumpla:
 .
.
Por ejemplo, dada la función:
Planteando y resolviendo la ecuación:
Se tiene que 2 y 4 son raíces (ver ecuación de segundo grado) ya que f(2) = 0 y f(4) = 0.
Buscando raíces.
- Dado el caso de que tanto el dominio como la imagen de la función sean los números reales (denominadas funciones reales) entonces los puntos en los que el gráfico corta al eje de las abscisas es una interpretación gráfica de las raíces de dicha función.
- El teorema fundamental del álgebra determina que todo polinomio en una variable compleja y de grado n tiene n raíces (contando sus multiplicidades). Aun así, Las raíces de los polinomios reales no son necesariamente reales; algunas de ellas, o incluso todas, pueden ser complejas.
- Una función trascendente como por ejemplo
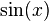 posee una infinidad de raíces, concretamente cualquier
posee una infinidad de raíces, concretamente cualquier  es raíz de esa función. En cambio la función
es raíz de esa función. En cambio la función 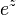 no se anula nunca sobre los números complejos.
no se anula nunca sobre los números complejos.
- El número de raíces de una función holomorfa o una función analítica es un conjunto numerable sin puntos de acumulación.
- Uno de los problemas no resueltos más interesantes de la matemática moderna es encontrar las raíces de la función zeta de Riemann.
Teorema del factor y del residuo.
Teorema del factor:
El polinomio P(x) es divisible por un polinomio de la forma (x - a) si y sólo si P(x = a) = 0.
Al valor x = a se le llama raíz o cero de P(x).
Las raíces o ceros de un polinomio son los valores que anulan el polinomio.
Teorema del residuo:
Teorema que establece que si un polinomio de x, f(x), se divide entre (x - a), donde a es cualquier número real o complejo, entonces el residuo es f(a).
Por ejemplo, si f(x) = x2 + x - 2 se divide entre (x-2), el residuo es f(2) = 22 + (2) - 2 = 4. Este resultado puede volverse obvio si cambiamos el polinomio a una de las siguientes formas equivalentes:
f(x) = (x-2)(x+3) + 4
Como se muestra, la expresión anterior nos puede llevar fácilmente a esperar que 4 sea el residuo cuando f(x) se divide entre (x-2).
El teorema del residuo nos puede ayudar a encontrar los factores de un polinomio. En este ejemplo, f(1) = 12 + (1) - 2 = 0. Por lo tanto, significa que no existe residuo, es decir, (x-1) es un factor. Esto puede mostrarse fácilmente una vez que reacomodamos el polinomio original en una de las siguientes expresiones equivalentes:
f(x) = (x-1)(x+2)
Como se muestra, (x-1) es un factor.
DIVISIÓN SINTÉTICA
La división sintética se realiza para simplificar la división de un polinomio entre otro polinomio de la forma x – c, logrando una manera mas compacta y sencilla de realizar la división.
Ilustraremos como el proceso de creación de la división sintética con un ejemplo:
Comenzamos dividiéndolo normalmente
Pero resulta mucho escribir pues repetimos muchos términos durante el procedimiento, los términos restados
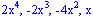
pueden quitarse sin crear ninguna confusión, al igual que no es necesario bajar los términos
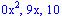
. al eliminar estos términos repetidos el ejercicio nos queda:
Ahora si mantenemos las potencias iguales de x en las columnas de cada potencia y colocando 0 en las faltantes se puede eliminar el escribir las potencias de x, así:
Como para este tipo de división solo se realiza con para divisores de la forma x – c entonces los coeficientes de la parte derecha siempre son 1 – c, por lo que podemos descartar el coeficiente 1 y el signo negativo, también se puede lograr una forma más compacta al mover los números hacia arriba, nos queda de la siguiente forma:
Si ahora insertamos a la primera posición del último renglón al primer coeficiente del residuo (2), tenemos que los primeros números de este renglón son los mismos coeficientes del cociente y el último número es el residuo, como evitamos escribir dos veces eliminamos el cociente.
Esta última forma se llama división sintética, pero ¿como hacerla sin tanto paso?, ahora les presentamos los pasos para llevar a cavo la división sintética:
Se ordenan los coeficientes de los términos en un orden decreciente de potencias de x hasta llegar al exponente cero rellenando con coeficientes cero donde haga falta
Después escribimos “c” en la parte derecha del renglón
Se baja el coeficiente de la izquierda al tercer renglón.
Multiplicamos este coeficiente por “c” para obtener el primer numero del segundo renglón (en el primer espacio de la izquierda nunca se escribe nada).
Simplificamos de manera vertical para obtener el segundo número de el tercer renglón.
Con este último número repetimos los pasos cuatro y cinco hasta encontrar el último número del tercer renglón, que será el residuo.
TEOREMA FUNDAMENTAL DEL ALGEBRA
El teorema fundamental del álgebra establece que un polinomio en una variable, no constante y con coeficientes complejos, tiene tantas raíces1 como indica su grado, contando las raíces con sus multiplicidades. En otras palabras, dado un polinomio complejo  de grado
de grado 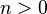 , la ecuación
, la ecuación  tiene exactamente
tiene exactamente  soluciones complejas, contando multiplicidades. De manera equivalente:
soluciones complejas, contando multiplicidades. De manera equivalente:
- El cuerpo de los complejos es cerrado para las operaciones algebraicas.
- Todo polinomio complejo de grado n se puede expresar como un producto de n polinomios de la forma
 .
.
El teorema se establece comúnmente de la siguiente manera:
Todo polinomio en una variable de grado n ≥ 1 con coeficientes reales o complejos tiene por lo menos una raíz (real o compleja).2
|
Aunque ésta en principio parece ser una declaración más débil, implica fácilmente la forma completa por la división polinómica sucesiva por factores lineales.
El nombre del teorema es considerado ahora un error por muchos matemáticos, puesto que es más un teorema del análisis matemático que del álgebra.
TEOREMA DE FACTORIZACIÓN LINEAL.
Si f(x) es un polinomio de grado n, con n > 0, entonces f(x) tiene precisamente n
factoreslineales, es decir:
f(x) = a(x – c
1)(x – c
2)….(x – c
n),
en donde c
1, c
2,…..cn son números complejos y a es el coeficiente principal de f(x)
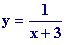 donde el denominador es cero para x = -3. Por tanto el dominio de esta función es
donde el denominador es cero para x = -3. Por tanto el dominio de esta función es 
 .
.

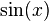 posee una infinidad de raíces, concretamente cualquier
posee una infinidad de raíces, concretamente cualquier  es raíz de esa función. En cambio la función
es raíz de esa función. En cambio la función 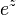 no se anula nunca sobre los números complejos.
no se anula nunca sobre los números complejos. de grado
de grado 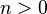 , la ecuación
, la ecuación  tiene exactamente
tiene exactamente  soluciones complejas, contando multiplicidades. De manera equivalente:
soluciones complejas, contando multiplicidades. De manera equivalente: .
.