En matemáticas, una función es el término usado para indicar la relación o correspondencia entre dos o más cantidades. Por ejemplo: el área A de un círculo es función de su radio r: el valor del área es proporcional al cuadrado del radio, A=π·r2
La manera habitual de denotar una función f es:
- f: A → B
- a → f(a),
donde A es el dominio de la función f, su primer conjunto o conjunto de partida; B es el codominio de f, su segundo conjunto o conjunto de llegada. Por f(a) se denota la regla o algoritmo para obtener la imagen de un cierto objeto arbitrario a del dominio A, es decir, el (único) objeto de Bque le corresponde. En ocasiones esta expresión es suficiente para especificar la función por completo, infiriendo el dominio y codominio por el contexto. En el ejemplo anterior, las funciones «cuadrado» e «inicial», llámeseles f y g, se denotarían entonces como:
- f: Z → N
- k → k2, o sencillamente f(k) = k2;
- g: V → A
- p → Inicial de p;
si se conviene V = {Palabras del español} y A = {Alfabeto español}.
Una función puede representarse de diversas formas: mediante el citado algoritmo para obtener la imagen de cada elemento, mediante una tabla de valores que empareje cada valor de la variable independiente con su imagen —como las mostradas arriba—, o como una gráfica que dé una imagen de la función.
Ejemplo 1
Correspondencia entre las personas que trabajan en una oficina y su peso expresado en kilos
Conjunto X
|
Conjunto Y
|
Ángela
|
55
|
Pedro
|
88
|
Manuel
|
62
|
Adrián
|
88
|
Roberto
|
90
|
Cada persona (perteneciente al conjunto X o dominio) constituye lo que se llama la entrada o variable independiente. Cada peso (perteneciente al conjunto Y o codominio) constituye lo que se llama la salida o variable dependiente. Notemos que una misma persona no puede tener dos pesos distintos. Notemos también que es posible que dos personas diferentes tengan el mismo peso.
Con estos ejemplos vamos entendiendo la noción de función: como vemos, todos y cada uno de los elementos del primer conjunto(X) están asociados a uno, y sólo a uno, del segundo conjunto (Y). Todos y cada uno significa que no puede quedar un elemento en X sin su correspondiente elemento en Y. A uno y sólo a uno significa que a un mismo elemento en X no le pueden corresponder dos elementos distintos en Y.
Ahora podemos enunciar una definición más formal:
Una función (f) es una regla que asigna a cada elemento x de un conjunto X (dominio) exactamente un elemento, llamado f(x), de un conjunto Y (codominio).
Otra definición equivalente es: sean X e Y dos conjuntos. Una función de X en Y es una regla (o un método) que asigna un (y sólo uno) elemento en Y a cada elemento en X.
Usualmente X e Y son conjuntos de números.
Generalizando, si se tiene una función f, definida de un conjunto A en un conjunto B, se anota
f : A -----> B (o, usando X por A e Y por B f : X -----> Y) o f(x) = x
Recordemos de nuevo que el primer conjunto A se conoce como dominio (Dom) de la función y B es el codominio o conjunto de llegada.
f(x) denota la imagen de x bajo f, mientras que x es la preimagen de f(x).
El rango (Rg) o recorrido (Rec) o ámbito (A) es el conjunto de todos los valores posibles de f(x) que se obtienen cuando x varía en todo el dominio de la función.
Dominio y rango de una función
Como ya vimos, el dominio de una función es el conjunto de valores para los cuales la función está definida; es decir, son todos los valores que puede tomar la variable independiente (la x).
Por ejemplo la función f(x) = 3x2 – 5x está definida para todo número real (x puede ser cualquier número real). Así el dominio de esta función es el conjunto de todos los números reales.
En cambio, la función 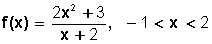 tiene como dominio todos los valores de x para los cuales −1< x < 2, porque aunque pueda tomar cualquier valor real diferente de –2, en su definición determina en qué intervalo está comprendida.
tiene como dominio todos los valores de x para los cuales −1< x < 2, porque aunque pueda tomar cualquier valor real diferente de –2, en su definición determina en qué intervalo está comprendida.
Si el dominio no se específica, debe entenderse que el dominio incluye a todos los números reales para los cuales la función tiene sentido.
En el caso de la función 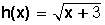 , el dominio de esta función son todos los números reales mayores o iguales a –3, ya que x + 3 debe ser mayor o igual que cero para que exista la raíz cuadrada.
, el dominio de esta función son todos los números reales mayores o iguales a –3, ya que x + 3 debe ser mayor o igual que cero para que exista la raíz cuadrada.
Como resumen, para determinar el dominio de una función, debemos considerar lo siguiente:
Si la función tiene radicales de índice par, el dominio está conformado por todos los números reales para los cuales la cantidad subradical sea mayor o igual a cero.
Si la función es un polinomio; una función de la forma f(x) = a0 + a1x + a2x2 +...+ anxn (donde a0, a1, a2,..., an son constantes y nun entero no negativo), el dominio está conformado por el conjunto de todos los números reales.
Si la función es racional; esto es, si es el cociente de dos polinomios, el dominio está conformado por todos los números reales para los cuales el denominador sea diferente de cero.
El rango (recorrido o ámbito) es el conjunto formado por todas las imágenes; es decir, es el conjunto conformado por todos los valores que puede tomar la variable dependiente; estos valores están determinados además, por el dominio de la función.

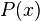 es un polinomio definido para todo número real
es un polinomio definido para todo número real  ; es decir, una suma finita de potencias de
; es decir, una suma finita de potencias de  multiplicados por coeficientes reales, de la forma:1
multiplicados por coeficientes reales, de la forma:1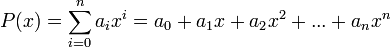

 , con
, con  . Sus representaciones gráficas son las famosas parábolas. Hay dos posibles representaciones que dependen del signo de
. Sus representaciones gráficas son las famosas parábolas. Hay dos posibles representaciones que dependen del signo de  . Son éstas:
. Son éstas:

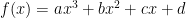 , con
, con  . Hay cuatro posibles representaciones gráfica de este tipo de funciones que dependen del signo de
. Hay cuatro posibles representaciones gráfica de este tipo de funciones que dependen del signo de  y de la relación entre
y de la relación entre 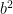 y
y  . Por tanto, para poder representarlas debemos tener en cuenta sus coeficientes. Os dejo una tabla con las cuatro gráficas posibles:
. Por tanto, para poder representarlas debemos tener en cuenta sus coeficientes. Os dejo una tabla con las cuatro gráficas posibles:



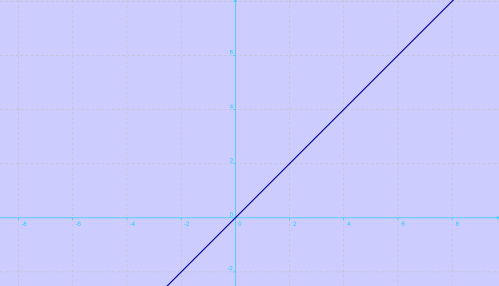
 , se llama función inversa de
, se llama función inversa de  y se denota por
y se denota por  a otra función que para cualquier valor del dominio de
a otra función que para cualquier valor del dominio de 
 , proviene de un único valor del dominio
, proviene de un único valor del dominio  .
.
 e
e  .
.
